Boats Model-boat Making Etcetera
Leaving the subject of ancient ships and navigation, we shall now turn our attention to the more recent doings of man on the ocean, and, before entering into the details of ships and ship-building, devote a little
time and space to the consideration of boats.
There are great varieties of boats—as regards shape, size, material, and use—so that it is not easy to decide on which we shall first fix our attention. There are large and small, long and short boats; flat, round, sharp, and bluff ones,—some clumsy, others elegant. Certain boats are built for carrying cargo, others for purposes of war. Some are meant for sailing, some for rowing; and while many kinds are devoted to business, others are intended solely for pleasure. Before we refer to any of these, perhaps our young readers will not object to be told how to construct:—
A Model Boat.
We need scarcely say that it is not expedient for a boy to attempt to build a model boat in the same manner as a regular boat-builder constructs one for actual service. It would be undertaking an unnecessary amount of labour to lay a keel and form ribs and nail on planks in the orthodox fashion, because, for all practical purposes, a boat cut out of a solid block of wood is quite as useful, and much more easily made.
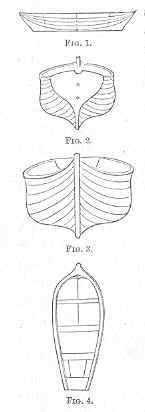
The first thing you have to do, my young boat-builder, then, is to go and visit a harbour or beach where varieties of boats are to be found, and, having settled in your mind which of them you intend to copy, make a careful drawing, in outline, of its form in four different positions. First, a side view, as in Figure 1. Then the stern, with the swelling sides of the boat visible, as in Figure 2. The bow, as in Figure 3; and a bird’s-eye view, as in Figure 4. The last drawing can be made by mounting on some neighbouring eminence, such as a bank or a larger boat, or, if that is impossible, by getting upon the stern of the boat itself, and thus looking down on it. These four drawings will be of great service in enabling you to shape your model correctly; for as you proceed with the carving you can, by holding the model up in the same position with any of the drawings, ascertain whether you are progressing properly; and if you get the correct form of your boat in these four positions, you will be almost certain to make a good boat. If, on the other hand, you go to work without drawings, the probability is that your boat will be lopsided, which will prevent it from floating evenly; or crooked, which will tend to check its speed in sailing, besides being clumsy and not “ship-shape,” as the sailors have it.
Figure 1 will keep you right in regard to relative length and depth; Figure 2 in regard to shape of stern and bulge of the sides; Figure 3 secures correct form of the bow; and Figure 4 enables you to proportion the breadth to the length.
The next thing to be done is to procure a block of fir-wood, with as few knots in it as possible, and straight in the grain. The size is a matter of choice—any size from a foot to eighteen inches will do very well for a model boat. Before beginning to carve this, it should be planed quite smooth and even on all sides, and the ends cut perfectly square, to permit of the requisite pencil-drawings being made on it.
The tools required are a small tenon-saw, a chisel, two or three gouges of different sizes, a spoke-shave, and a file with one side flat and the other round. A rough rasp-file and a pair of compasses will also be found useful. All of these ought to be exceedingly sharp. The gouges and the spoke-shave will be found the most useful of these implements.
Begin by drawing a straight line with pencil down the exact centre of what will be the deck; continue it down the part that will be the stern; then carry it along the bottom of the block, where the keel will be, and up the front part, or bow. If this line has been correctly drawn, the end of it will exactly meet the place where you began to draw it. On the correctness of this line much will depend; therefore it is necessary to be careful and precise in finding out the 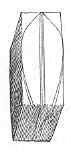 centre of each surface of the block with the compasses. Next, draw a line on each side of this centre line (as in the accompanying diagram), which will give the thickness of the keel and stern-post. Then on the upper surface of the block draw the form of the boat to correspond with the bird’s-eye view (Figure 4, on page 82) already referred to. Then draw one-half of the stern on a piece of thin card-board, and when satisfied that it is correct cut it out with scissors; apply it to the model, first on one side, and then on the other side of the stern-post. By thus using a pattern of only one-half of the stern, exact uniformity of the two sides is secured. Treat the bow in the same way. Of course the pattern of the bow will at first be drawn on the flat surface of the block, and it will represent not the actual bow, but the thickest part of the hull, as seen in the position of Figure 3, on page 82. After this, turn the side of the block, and draw the form represented in Figure 1, page 82, thereon, and mark on the keel the point where the stem and keel join, and also where the stern and keel join. This is necessary, because in carving the sides of the boat these lines will be among the first to be cut away. The next proceeding is to cut away at the sides and bottom of the block until, looking at it in the proper positions, the bow resembles Figure 3, and the stern Figure 2, above referred to. This will be done chiefly with the gouge, the chisel and spoke-shave being reserved for finishing. Then saw off the parts of the bow and stern that will give the requisite slope to these parts, being guided by the marks made on the keel. In cutting away the upper parts of the bow and stern, be guided by the curved lines on the deck; and in forming the lower parts of the same portions, keep your eye on your drawing, which is represented by Figure 1.
centre of each surface of the block with the compasses. Next, draw a line on each side of this centre line (as in the accompanying diagram), which will give the thickness of the keel and stern-post. Then on the upper surface of the block draw the form of the boat to correspond with the bird’s-eye view (Figure 4, on page 82) already referred to. Then draw one-half of the stern on a piece of thin card-board, and when satisfied that it is correct cut it out with scissors; apply it to the model, first on one side, and then on the other side of the stern-post. By thus using a pattern of only one-half of the stern, exact uniformity of the two sides is secured. Treat the bow in the same way. Of course the pattern of the bow will at first be drawn on the flat surface of the block, and it will represent not the actual bow, but the thickest part of the hull, as seen in the position of Figure 3, on page 82. After this, turn the side of the block, and draw the form represented in Figure 1, page 82, thereon, and mark on the keel the point where the stem and keel join, and also where the stern and keel join. This is necessary, because in carving the sides of the boat these lines will be among the first to be cut away. The next proceeding is to cut away at the sides and bottom of the block until, looking at it in the proper positions, the bow resembles Figure 3, and the stern Figure 2, above referred to. This will be done chiefly with the gouge, the chisel and spoke-shave being reserved for finishing. Then saw off the parts of the bow and stern that will give the requisite slope to these parts, being guided by the marks made on the keel. In cutting away the upper parts of the bow and stern, be guided by the curved lines on the deck; and in forming the lower parts of the same portions, keep your eye on your drawing, which is represented by Figure 1.
It is advisable to finish one side of the boat first, so that, by measurement and comparison, the other side may be made exactly similar. Those who wish to be very particular on this point may secure almost exact uniformity of the two sides by cutting out several moulds (three will be sufficient) in card-board. These moulds must be cut so as to fit three marked points on the finished side, as represented by three dotted lines on Figure 1; and then the unfinished side must be cut so as to fit the moulds at the corresponding points. If the two sides are quite equal at these three points, it is almost impossible to go far wrong in cutting away the wood between them—the eye will be a sufficient guide for the rest.
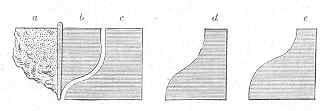
The accompanying diagram shows the three moulds referred to, one of them being nearly applied to the finished part of the hull to which it belongs. Thus—(a) represents the unfinished side of the boat; (b) the finished side; (c) is the mould or card cut to correspond with the widest part of the finished side, near the centre of the boat; (d) is the mould for the part near the bow; (e) for that near the stern. These drawings are roughly given, to indicate the plan on which you should proceed. The exact forms will depend on your own taste or fancy, as formed by the variously-shaped boats you have studied. And it may be remarked here, that all we have said in regard to the cutting out of model boats applies equally to model ships.

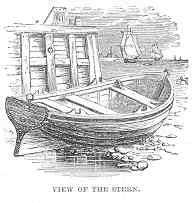
The outside of your boat having been finished, the bow having been fashioned somewhat like that represented in the accompanying cut, and the stern having been shaped like that shown in the illustration given below, the next thing to be done is to hollow out the hull. Care must be taken in doing this not to cut away too much wood from one part, or to leave too much at another; a little more than half an inch of thickness may be left everywhere. Next, fix in the thwarts, or seats, as in the foregoing cut, attach a leaden keel, and the boat is completed.
The keel may be formed by running melted lead into a groove cut in a piece of wood, or, better still, into a groove made in nearly dry clay. By driving four or five nails (well greased) into the groove before pouring in the melted lead, holes may be formed in the keel by simply withdrawing the nails after it is cold.
A mast and sail, however, are still wanted. The best kind of sail is the lug, which is an elongated square sail—shown in the accompanying illustration.

Most of our fishing-boats are provided with lug-sails, and on this account are styled luggers. These boats are of all sizes, some of them being fifty tons burden, and carrying crews of seven or ten men each. A picture of a lugger is given on the next page.
Great numbers of fishing-boats may be seen at Great Yarmouth, and all along the coasts of Norfolk and Suffolk. They are employed in the herring-fishery, and use nets, which are let down in deep water, corks floating the upper edges of the nets, and the lower edges being sunk by leads, so that they remain in the water perpendicularly like walls, and intercept the shoals of  herring when they chance to pass. Thousands of these glittering silvery fish get entangled in the meshes during night. Then the nets are drawn up, and the fish taken out and thrown into a “well,” whence they are removed as quickly as possible, and salted and packed in lockers; while the nets are let down again into the sea. These boats remain out usually a week at a time. Most of them return to port on Saturday, in order to spend Sunday as a day of rest. Some, however—regardless of the fact that He who gives them the fish with such liberal hand, also gave them the command, “Remember the sabbath day”—continue to prosecute the fishing on that day. But many a good man among the fishermen has borne testimony to the fact that these do not gain additional wealth by their act of disobedience; while they lose in the matter of nets (which suffer from want of frequent drying) and in the matter of health (which cannot be maintained so well without a weekly day of rest), while there can be no doubt that they lose the inestimable blessing of a good conscience. So true is it that godliness is profitable for the life which now is as well as for that which is to come.
herring when they chance to pass. Thousands of these glittering silvery fish get entangled in the meshes during night. Then the nets are drawn up, and the fish taken out and thrown into a “well,” whence they are removed as quickly as possible, and salted and packed in lockers; while the nets are let down again into the sea. These boats remain out usually a week at a time. Most of them return to port on Saturday, in order to spend Sunday as a day of rest. Some, however—regardless of the fact that He who gives them the fish with such liberal hand, also gave them the command, “Remember the sabbath day”—continue to prosecute the fishing on that day. But many a good man among the fishermen has borne testimony to the fact that these do not gain additional wealth by their act of disobedience; while they lose in the matter of nets (which suffer from want of frequent drying) and in the matter of health (which cannot be maintained so well without a weekly day of rest), while there can be no doubt that they lose the inestimable blessing of a good conscience. So true is it that godliness is profitable for the life which now is as well as for that which is to come.
A model boat should be rigged with only one mast and lug-sail, or with two masts and sails at the most. Three are unnecessary and cumbrous. Each sail should be fixed to a yard, which should be hoisted or hauled down by means of a block or pulley fastened near the top of the mast. The positions of these yards and the form of the sails may be more easily understood by a glance at our woodcut than by reading many pages of description.
Sprit-sails are sometimes used in boats. These are fore-and-aft sails, which are kept distended by a sprit instead of a yard. The sprit is a long pole, one end of which is fixed to the lowest innermost corner, near the mast, and the other end extending to the highest outermost corner; thus it lies diagonally across the sail. It is convenient when a boat “tacks,” or “goes about”—in other words, when it goes round frequently, and sails, now leaning on one side, and, at the next tack, on the other side. In this case the sprit requires little shifting or attention. But it is dangerous in squally weather, because, although the sheet or line which holds the lower and outer end of a sail may be let go for the sake of safety, the upper part remains spread to the wind because of the sprit.
The best rig of all for a model boat, and indeed for a pleasure-boat, is that which comprises a main-sail, in form like that of a sloop or a cutter, omitting the boom, or lower yard, and a triangular fore-sail extending from near the mast to the bow of the boat or to the end of the bowsprit—somewhat like a sloop’s jib. Both of the sails referred to may be seen at the part of this book which treats of sloops and cutters; and they are the same in form, with but slight modification, when applied to boats.
Racing-boats are long, low, narrow, and light. Some are so narrow as to require iron rowlocks extending a considerable distance beyond the sides of the boat for the oars to rest in. Many of these light craft may be seen on the Thames and Clyde, and other rivers throughout the kingdom. The larger sort do not require what we may call the outrigger rowlocks.
The “Rob Roy” canoe has, of late years, come much into fashion as a racing and pleasure boat. Whatever the advantages of this craft may be, it has this disadvantage, that it can hold only one person; so that it may be styled an unsocial craft, the company of one or more friends being impossible, unless, indeed, one or more canoes travel in company.
This species of canoe became celebrated some years ago, in consequence of an interesting and adventurous voyage of a thousand miles through Germany, Switzerland, and France, and, subsequently, through part of Norway and Sweden, made by Mr Macgregor in a craft of this kind, to which he gave the name of “Rob Roy.” Since the craft became popular, numerous and important improvements have been made in the construction of its hull and several parts, but its distinctive features remain unaltered. The “Rob Roy” canoe is, in fact, almost identical with the Eskimo kayak, except in regard to the material of which it is made—the former being composed wholly of wood, the latter of a framework of wood covered with skin. There is the same long, low, fish-like form, the same deck, almost on a level with the water, the same hole in the centre for the admission of the man, the same apron to keep out water, and the same long, double-bladed paddle, which is dipped on each side alternately. The “Rob Roy” has, however, the addition of a small mast, a lug-sail, and a jib. It has also a back-board, to support the back of the canoeman; the paddle, too, is somewhat shorter than that of the Eskimo canoe; and the whole affair is smarter, and more in accordance with the tastes and habits of the civilised men who use it.
In his various voyages, which we might almost style journeys, the originator of the “Rob Roy” canoe proved conclusively that there were few earthly objects which could form a barrier to his progress. When his canoe could not carry him, he carried it! Waterfalls could not stop him, because he landed below them, and carried his canoe and small amount of baggage to the smooth water above the falls. In this he followed the example of the fur-traders and Indians of North America, who travel over any number of miles of wilderness in this manner. Shallows could not stop him, because his little bark drew only a few inches of water. Turbulent water could not swamp him, because the waves washed harmlessly over his smooth deck, and circled innocently round his protective apron. Even long stretches of dry land could not stop him, because barrows, or carts, or railways could transport his canoe hither and thither with perfect ease to any distance; so that when the waters of one river failed him, those of the next nearest were easily made available. In conclusion, it may be said that the “Rob Roy” canoe is a most useful and pleasant craft for boys and young men, especially at those watering-places which have no harbour or pier, and where, in consequence of the flatness of the beach, boats cannot easily be used.
It  would be an almost endless as well as unprofitable task to go over the names and characteristics of all our various kinds of boats in detail.
would be an almost endless as well as unprofitable task to go over the names and characteristics of all our various kinds of boats in detail.
Of heavy-sterned and clumsy river craft, we have an innumerable fleet.
There are also Torbay Trawlers, which are cutters of from twenty to fifty tons; and the herring-boats of Scotland; and cobbles, which are broad, bluff, little boats; and barges, which are broad, bluff, large ones; and skiffs, and scows, and many others.
In foreign lands many curious boats are to be met with. The most graceful of them, perhaps, are those which carry lateen sails—enormous triangular sails, of which kind each boat usually carries only one.
India-rubber boats there are, which can be inflated with a pair of bellows, and, when full, can support half-a-dozen men or more, while, when empty, they can be rolled up and carried on the back of one man, or in a barrow. One boat of this kind we once saw and paddled in. It was made in the form of a cloak, and could be carried quite easily on one’s shoulders. When inflated, it formed a sort of oval canoe, which was quite capable of supporting one person. We speak from experience, having tried it some years ago on the Serpentine, and found it to be extremely buoyant, but a little given to spin round at each stroke of the paddle, owing to its circular shape and want of cut-water or keel.
Of all the boats that swim, the lifeboat is certainly one of the most interesting; perhaps it is not too much to add that it is also one of the most useful. But this boat deserves a chapter to itself.
Previous: The Mariner’s Compass—portuguese Discoveries
Next: Lifeboats And Lightships
|
|
| SHARE | |
 |
|
| ADD TO EBOOK |